Papers by Dipl. Inform. Alexander Schier

Curve embedding, Mesh proxies, Geodesic paths, UV seams, Texture transfer, Polygon soups}, abstract = {We present a numerically robust algorithm for augmenting inconsistent meshes and polygon soups with curves defined on a mesh proxy. Unlike prior approaches, which transfer only vertex positions to the proxy, our method represents input edges on the proxy by geodesic paths and merges them with proxy-defined edge paths such as UV seams. This enables reliable detection of intersections between geodesic paths and proxy seams and avoids explicit edge-edge intersection tests, which makes the construction stable even on poorly conditioned meshes. We demonstrate the method in texture transfer, where projected input faces are cut along UV seams of the proxy so that the reconstructed result mesh reproduces the proxy seam layout explicitly and avoids distortions that previous approaches could only mitigate heuristically. To construct this result mesh, we first build an overlay curve network consisting of geodesic segments and proxy seam edges, and then reconstruct a manifold mesh aligned with the input mesh. Our experiments show that this reconstruction removes seam artifacts and reduces the associated high-distortion outliers of prior heuristic methods. Beyond UV seams, the construction can be used more generally to transfer proxy-defined curves onto disjoint meshes, such as collections of NURBS patches.

Generative AI's function as a frictionless "answer engine" creates a paradox in educational HCI: the very tools that can enhance intellect may also weaken it by allowing users to circumvent crucial cognitive processes. This risks creating a "hollowed mind"—knowledge that is broad but superficial, and a user experience that diminishes learner agency. The convenience of cognitive offloading introduces a motivational challenge that traditional cognitive scaffolding cannot address. We argue that designing genuine human-AI partnerships in learning requires moving beyond cognitive support to motivation-aware scaffolding. This paper provides a toolkit for building motivation-aware AI systems. At its core is the Dual Zone of Proximal Development (DZPD), a conceptual framework building on foundational work in educational psychology. We introduce an overarching design principle, concrete design principles, illustrative archetypes, and examples of measurable indicators. These conceptual tools offer essential guidance for the next wave of empirical HCI research in education.

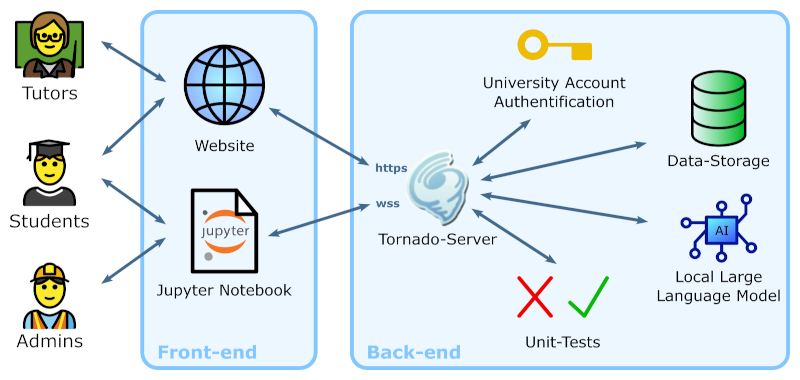
Grading student assignments in STEM courses is a laborious and repetitive task for tutors, often requiring a week to assess an entire class. For students, this delay of feedback prevents iterating on incorrect solutions, hampers learning, and increases stress when exercise scores determine admission to the final exam. Recent advances in AI-assisted education, such as automated grading and tutoring systems, aim to address these challenges by providing immediate feedback and reducing grading workload. However, existing solutions often fall short due to privacy concerns, reliance on proprietary closed-source models, lack of support for combining Markdown, LaTeX and Python code, or excluding course tutors from the grading process. To overcome these limitations, we introduce PyEvalAI, an AI-assisted evaluation system, which automatically scores Jupyter notebooks using a combination of unit tests and a locally hosted language model to preserve privacy. Our approach is free, open-source, and ensures tutors maintain full control over the grading process. A case study demonstrates its effectiveness in improving feedback speed and grading efficiency for exercises in a university-level course on numerics.

We introduce an interactive comic chat system that seamlessly integrates visual storytelling with text-based real-time interaction to enhance digital communication. Our approach employs generative {AI} to create interactive comics, supporting the easy creation of personalized characters and scenes, dynamically adapting these personalized characters and environments to chat content and additional user input, automating the generation of visually coherent comic panels, and overcoming the limitations of previous comic chat systems that are limited to pre-defined graphical elements. In addition, the chat system incorporates interactive elements such as chat bots and themed rooms to increase user engagement. In a user study, we show that our novel system can enhance users’ ability to convey emotions and engage in meaningful interactions online, and that users appreciate the wide range of self-expression options and personalized characters that allow for more nuanced communication. The versatility of generative {AI} approaches makes our platform suitable for a wide range of applications beyond mere chatting, including education, reducing language barriers and character-driven role-playing games.

Discrete exterior calculus (DEC) is a numerical method for solving partial differential equations on meshes with applications in computer graphics, numerics, and physical simulations. It discretizes PDEs in a way such that important integral theorems hold exactly instead of being approximated. The drawback of the method is that it has strong requirements on the mesh. While the narrow range of admissible meshes mentioned in the original work could be widened, current methods still exclude an essential category of meshes, i.e., meshes with concyclic triangle pairs. Such meshes are common, as many synthetic meshes, e.g., triangulations of CAD models, handcrafted 3D models, and even results of surface meshing algorithms, contain such triangle pairs. Our paper describes an approach that allows us to use meshes with arbitrary triangulations that may contain concyclic triangle pairs by defining DEC operators for concyclic polygons.

We present an efficient approach for the parameterization of triangle soups. Our technique tackles the problem by first approximating the triangle soup by a watertight 2-manifold offset mesh proxy. By establishing point correspondences between the triangle soup and the shape proxy by tracing electrostatic field lines in time O(kn) instead of O(kn^2), we can transfer properties computed on the surface, such as UV-coordinates even for large input meshes. The technique can process large triangle soups by replacing the computational intensive physical calculations by approximations developed initially for large-scale physical simulations. Thus it is possible to decrease the time complexity of the initial charge distribution algorithm from O(n3) to O(n). We demonstrate our method on a multitude of challenging triangle soups and focus on the transfer of UV-coordinates during our experiments. An intensive run-time analysis and a comparison of our results to state of the art techniques in standard modeling tools concludes our study.

We present the discrete exterior calculus (DEC) to solve discrete partial differential equations on discrete objects such as cell complexes. To cope with advection-dominated problems, we introduce a novel stabilization technique to the DEC. To this end, we use the fact that the DEC coincides in special situations with known discretization schemes such as finite volumes or finite differences. Thus, we can carry over well-established upwind stabilization methods introduced for these classical schemes to the DEC. This leads in particular to a stable discretization of the Lie-derivative. We present the numerical features of this new discretization technique and study its numerical properties for simple model problems and for advection-diffusion processes on simple surfaces.