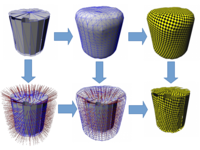
Fast texture mapping for triangle soups using electrostatic monopole field lines

Alexander Schier, Stefan Hartmann and Reinhard Klein.
Published in: Computers & Graphics, Vol 77, pages 140-155, 2018

Abstract

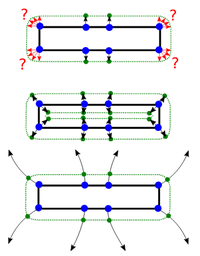
We present an efficient approach for the parameterization of triangle soups. Our technique tackles the problem by first approximating the triangle soup by a watertight 2-manifold offset mesh proxy. By establishing point correspondences between the triangle soup and the shape proxy by tracing electrostatic field lines in time O(kn) instead of O(kn²), we can transfer properties computed on the surface, such as UV-coordinates even for large input meshes. The technique can process large triangle soups by replacing the computational intensive physical calculations by approximations developed initially for large-scale physical simulations. Thus, it is possible to decrease the time complexity of the initial charge distribution algorithm from O(n³) to O(n). We demonstrate our method on a multitude of challenging triangle soups and focus on the transfer of UV-coordinates during our experiments. An intensive run-time analysis and a comparison of our results to state of the art techniques in standard modeling tools concludes our study.

Keywords: Parameterization, Point Correspondences, Seamless Mapping, Texturing, Triangle Soups

Links: [paper]¹ [paper (lowres images)]¹ [errata] [bibtex] [published in CAG] [university page] [DOI:10.1016/j.cag.2018.09.020]

Images

Our parameterization pipeline for triangle soups

Some example triangle soups parameterized using our approach

Point correspondences using different vertex mapping methods. From top to bottom:
Distance based, using dipole fields (Degener and Klein), and using monopole fields (our method)

A comparison of our fully automatic method with a manual parametrization by an expert using Autodesk Maya®

A noisy mesh of a botijo parameterized using field lines (red) to find point correpondences on a 2-manifold offset mesh proxy

Bibtex

@ARTICLE{schier2018fast,
    author = {Schier, Alexander and Hartmann, Stefan and Klein, Reinhard},
     pages = {140--155},
     title = {Fast texture mapping for triangle soups using electrostatic monopole field lines},
   journal = {Computers {\&} Graphics},
    volume = {77},
      year = {2018},
  keywords = {Parameterization, Point Correspondences, Seamless Mapping, Texturing, Triangle Soups},
  abstract = {We present an efficient approach for the parameterization of triangle soups. Our technique tackles
              the problem by first approximating the triangle soup by a watertight 2-manifold offset mesh proxy.
              By establishing point correspondences between the triangle soup and the shape proxy by tracing
              electrostatic field lines in time O(kn) instead of O(kn^2), we can transfer properties computed on
              the surface, such as UV-coordinates even for large input meshes. The technique can process large
              triangle soups by replacing the computational intensive physical calculations by approximations
              developed initially for large-scale physical simulations. Thus, it is possible to decrease the time
              complexity of the initial charge distribution algorithm from O(n^3) to O(n). We demonstrate our
              method on a multitude of challenging triangle soups and focus on the transfer of UV-coordinates
              during our experiments. An intensive run-time analysis and a comparison of our results to state of
              the art techniques in standard modeling tools concludes our study.},
      issn = {0097-8493},
       url = {https://schier.info/papers/fast_texture_mapping.pdf},
       doi = {https://doi.org/10.1016/j.cag.2018.09.020}
}

Errata

The x-axis in Fig. 12 shows the number of field lines and not the number of triangles. In all our example models, the number of triangles is exactly twice the number of field lines, so the convergence rate is the same. The error is corrected in the interactive plots below.
The denominator of the fraction in the definition of the potential φ in Eq. 1 and its discrete approximation I_ij in section 7.4 should not be squared. The correct equations are:

$ϕ (\vec{x}) = k_{e} \int_{Γ} σ (\vec{y}) \frac{1}{| \vec{x} - \vec{y} |} d y$
and
$I_{i j} := \sum_{k = 1}^{m} w_{k} \frac{1}{| {\vec{c}}_{i} - {\vec{y}}_{j k} |}$ .

All results were computed using the correct formula.

Plots

¹ Author's version (accepted manuscript)